Rectified Linear Unit

Note

A Rctified Linear Unit is usually called ReLU.

Introduction

ReLU is one of most frequently used activations for hidden layers because of the following two reasons.

1. Using ReLU typically avoids gradient vanishing/exploding.

2. Because of how simple ReLU is, networks with ReLU train quite fast compared to more complicated activation functions like \( Tanh \).

Definition

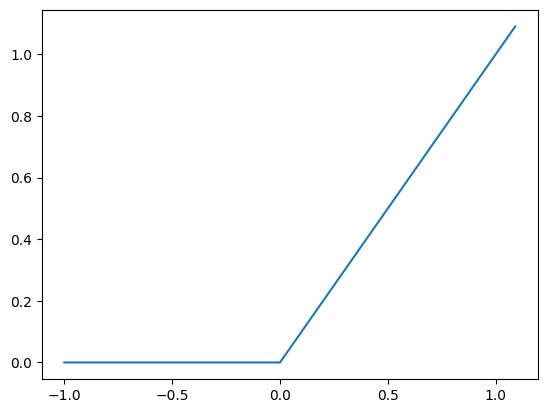
ReLU(\( x \)) = \( \max \{ 0, x \} \)

How does ReLU look, and how it works in code?

%matplotlib inline

import numpy as np
from matplotlib import pyplot as plt

def ReLU(x):
    return np.maximum(0, x)

x = np.arange(-10, 11)
y = ReLU(x)
print("x = ", x)
print("y = ", y)

x =  [-10  -9  -8  -7  -6  -5  -4  -3  -2  -1   0   1   2   3   4   5   6   7
   8   9  10]
y =  [ 0  0  0  0  0  0  0  0  0  0  0  1  2  3  4  5  6  7  8  9 10]

See how all negative numbers are replaced by 0.

How does ReLU’s input-output looks like?

x = np.arange(-100, 110) / 100
y = ReLU(x)
plt.plot(x, y)
plt.show()